[,1] [,2]
[1,] 0.2655087 0.6547239
[2,] 0.3721239 0.3531973
[3,] 0.5728534 0.2702601
[4,] 0.9082078 0.9926841
[5,] 0.2016819 0.6334933
[6,] 0.8983897 0.213208118 Réseaux neuronaux
Dans ce chapitre, nous allons explorer plusieurs visualisations des données de l’algorithme d’apprentissage par descente de gradient pour les réseaux neuronaux.
Plan du chapitre :
- Nous commençons par simuler et visualiser quelques données 2d pour une classification binaire.
- Nous montrons ensuite comment une fonction de classification en 2d peut être visualisée en calculant les prédictions sur une grille, puis en utilisant la fonction de classification en 2d.
geom_tile()ougeom_path()avec des lignes de contour. - Nous calculons les prédictions du modèle linéaire et les mises à jour de la descente de gradient à l’aide d’un système simple de différenciation automatique (auto-grad).
- Nous terminons en implémentant la descente de gradient pour un réseau neuronal, et en utilisant une visualisation des données interactive pour montrer comment les prédictions deviennent plus précises avec les itérations de l’algorithme d’apprentissage.
18.1 Visualisation des données simulées
Dans cette section, nous simulons un ensemble de données simple avec un motif non linéaire pour la classification binaire.
Dans la simulation, le tableau de données ci-dessus comporte les caractéristiques “cachées” qui sont utilisées pour créer les étiquettes, mais ne sont pas disponibles pour l’apprentissage. La fonction latente/vraie utilisée pour la classification est la suivante,
bayes <- function(DT)DT[, (V1>0.2 & V2<0.8)]
library(data.table)
hidden.dt <- data.table(features.hidden)
label.vec <- ifelse(bayes(hidden.dt), 1, -1)
table(label.vec)label.vec
-1 1
31 69 Les étiquettes binaires ci-dessus sont créées à partir des caractéristiques cachées, mais pour l’apprentissage, nous n’avons accès qu’aux caractéristiques bruitées ci-dessous,
[,1] [,2]
[1,] 0.2341860 0.6237056
[2,] 0.3813061 0.3553031
[3,] 0.5310719 0.2247141
[4,] 0.9879718 1.0005855
[5,] 0.2181573 0.6007640
[6,] 0.8573663 0.3015725Pour tracer les données et visualiser le motif, nous utilisons le code ci-dessous,
library(animint2)
label.fac <- factor(label.vec)
sim.dt <- data.table(features.noisy, label.fac)
ggplot()+
geom_point(aes(
V1, V2, color=label.fac),
data=sim.dt)+
coord_equal()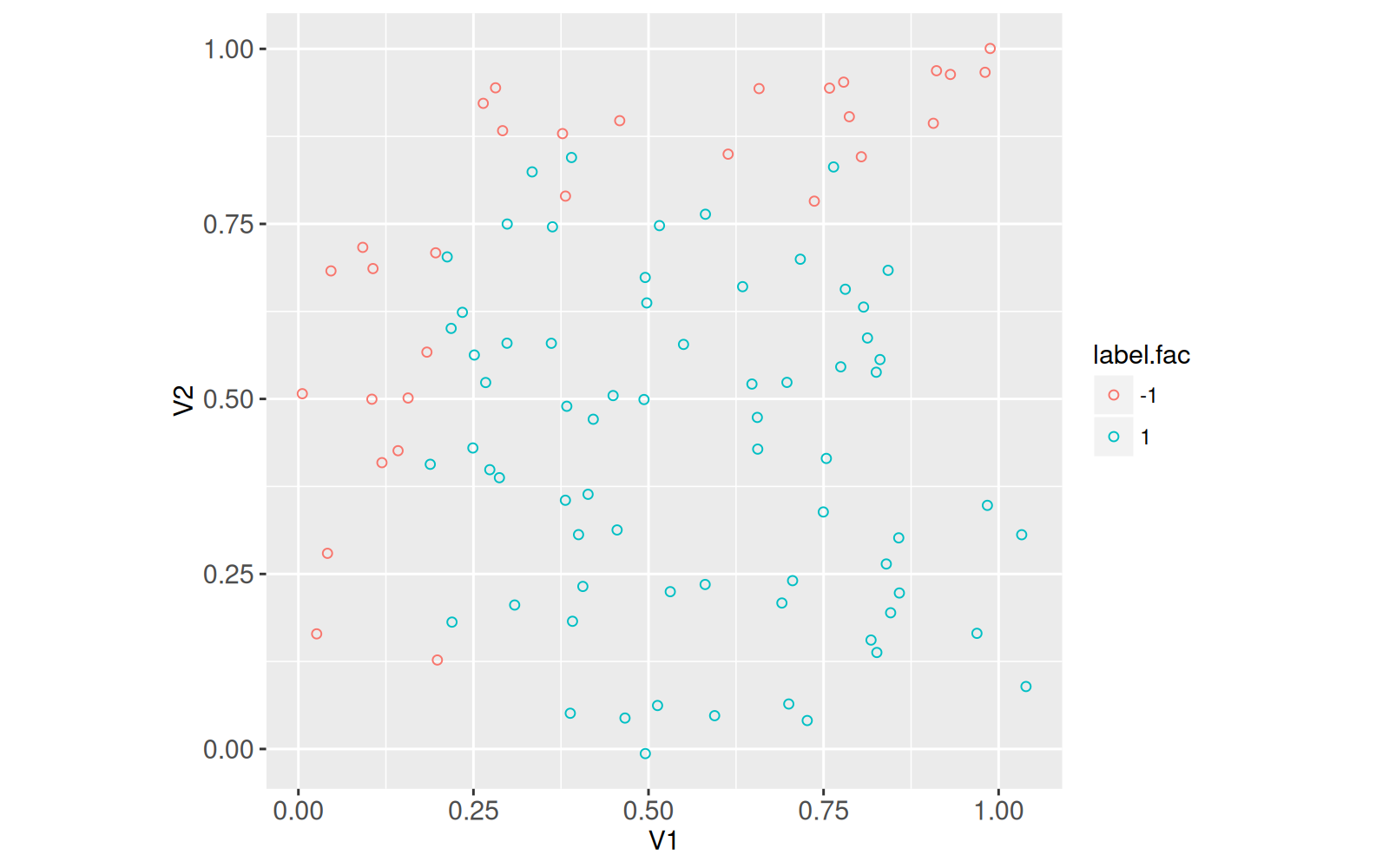
Le graphique ci-dessus montre chaque ligne de l’ensemble de données comme un point, avec les deux caractéristiques sur les deux axes, et les deux étiquettes dans deux couleurs différentes. La partie inférieure droite de l’espace des caractéristiques a tendance à avoir des étiquettes positives, et les zones gauche et supérieure ont des étiquettes négatives. Il s’agit du motif que le réseau neuronal va apprendre. Pour former correctement un réseau neuronal, nous devons diviser les données en deux ensembles :
- subtrain : utilisé pour calculer les gradients, qui servent à mettre à jour les paramètres de pondération, et les valeurs prédites. Avec un nombre suffisant d’itérations/époques de l’algorithme d’apprentissage par descente de gradient et un modèle de réseau neuronal suffisamment puissant (nombre suffisant d’unités/couches cachées), il devrait être possible d’obtenir une prédiction parfaite sur l’ensemble de sous-entraînement.
- validation : utilisée pour éviter le surajustement. En calculant l’erreur de prédiction sur l’ensemble de validation et en choisissant le nombre d’itérations/époques de descente du gradient qui minimise l’erreur de validation, nous pouvons nous assurer que le modèle appris possède de bonnes propriétés de généralisation (il fournit de bonnes prédictions non seulement sur l’ensemble de sous-entraînement, mais aussi sur de nouveaux points de données comme dans l’ensemble de validation).
set.vec
subtrain validation
50 50 Le code ci-dessus est utilisé pour affecter aléatoirement la moitié des données à chacun des ensembles de sous-entraînement et de validation. Ci-dessous, nous traçons les deux ensembles dans des facettes séparées,
sim.dt[, set := set.vec]
ggplot()+
facet_grid(. ~ set, labeller=label_both)+
geom_point(aes(
V1, V2, color=label.fac),
data=sim.dt)+
coord_equal()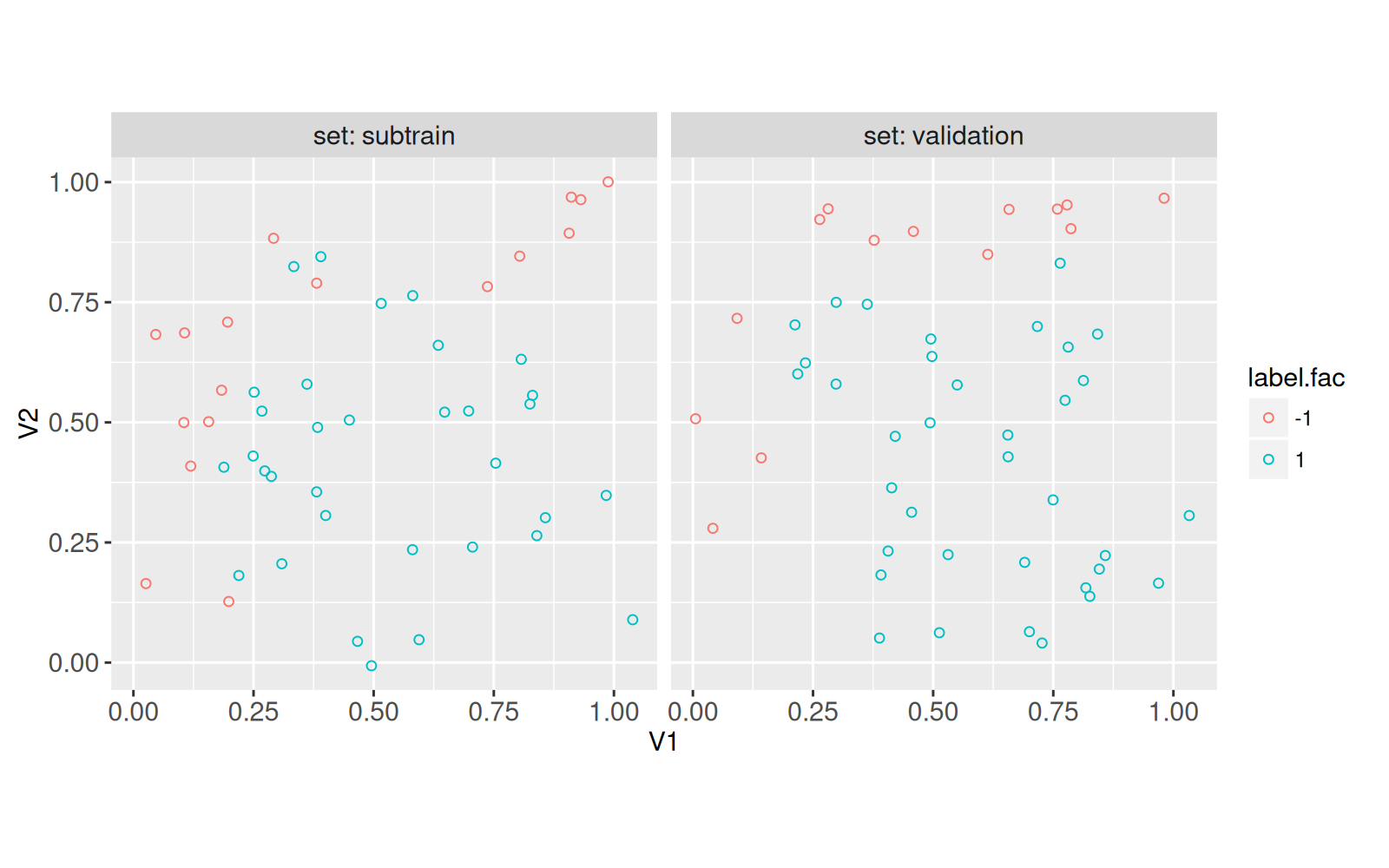
18.2 Visualiser la fonction de classification optimale de Bayes
Pour visualiser la limite de décision optimale/Bayes, nous devons évaluer la fonction sur une grille de points 2d qui couvre l’espace des caractéristiques. Pour créer une telle grille, nous commençons par créer une liste contenant les deux grilles 1d pour chaque caractéristique,
$V1
[1] 0.005600558 0.041238397 0.076876237 0.112514077 0.148151916 0.183789756
[7] 0.219427595 0.255065435 0.290703274 0.326341114 0.361978954 0.397616793
[13] 0.433254633 0.468892472 0.504530312 0.540168151 0.575805991 0.611443831
[19] 0.647081670 0.682719510 0.718357349 0.753995189 0.789633028 0.825270868
[25] 0.860908708 0.896546547 0.932184387 0.967822226 1.003460066 1.039097905
$V2
[1] -0.006562821 0.028166431 0.062895684 0.097624936 0.132354189
[6] 0.167083441 0.201812694 0.236541946 0.271271199 0.306000451
[11] 0.340729703 0.375458956 0.410188208 0.444917461 0.479646713
[16] 0.514375966 0.549105218 0.583834471 0.618563723 0.653292975
[21] 0.688022228 0.722751480 0.757480733 0.792209985 0.826939238
[26] 0.861668490 0.896397742 0.931126995 0.965856247 1.000585500Ensuite, nous utilisons CJ (cross-join) pour créer un tableau de données représentant la grille 2d, pour laquelle nous évaluons la fonction de classification best/Bayes,
V1 V2 bayes.num bayes.fac
1: 0.005600558 -0.006562821 -1 -1
2: 0.005600558 0.028166431 -1 -1
---
899: 1.039097905 0.965856247 -1 -1
900: 1.039097905 1.000585500 -1 -1Le meilleur classificateur est visualisé ci-dessous dans l’espace des caractéristiques,
ggplot()+
geom_tile(aes(
V1, V2, fill=bayes.fac),
color=NA,
data=grid.dt)+
geom_point(aes(
V1, V2, fill=label.fac),
color="black",
data=sim.dt)+
coord_equal()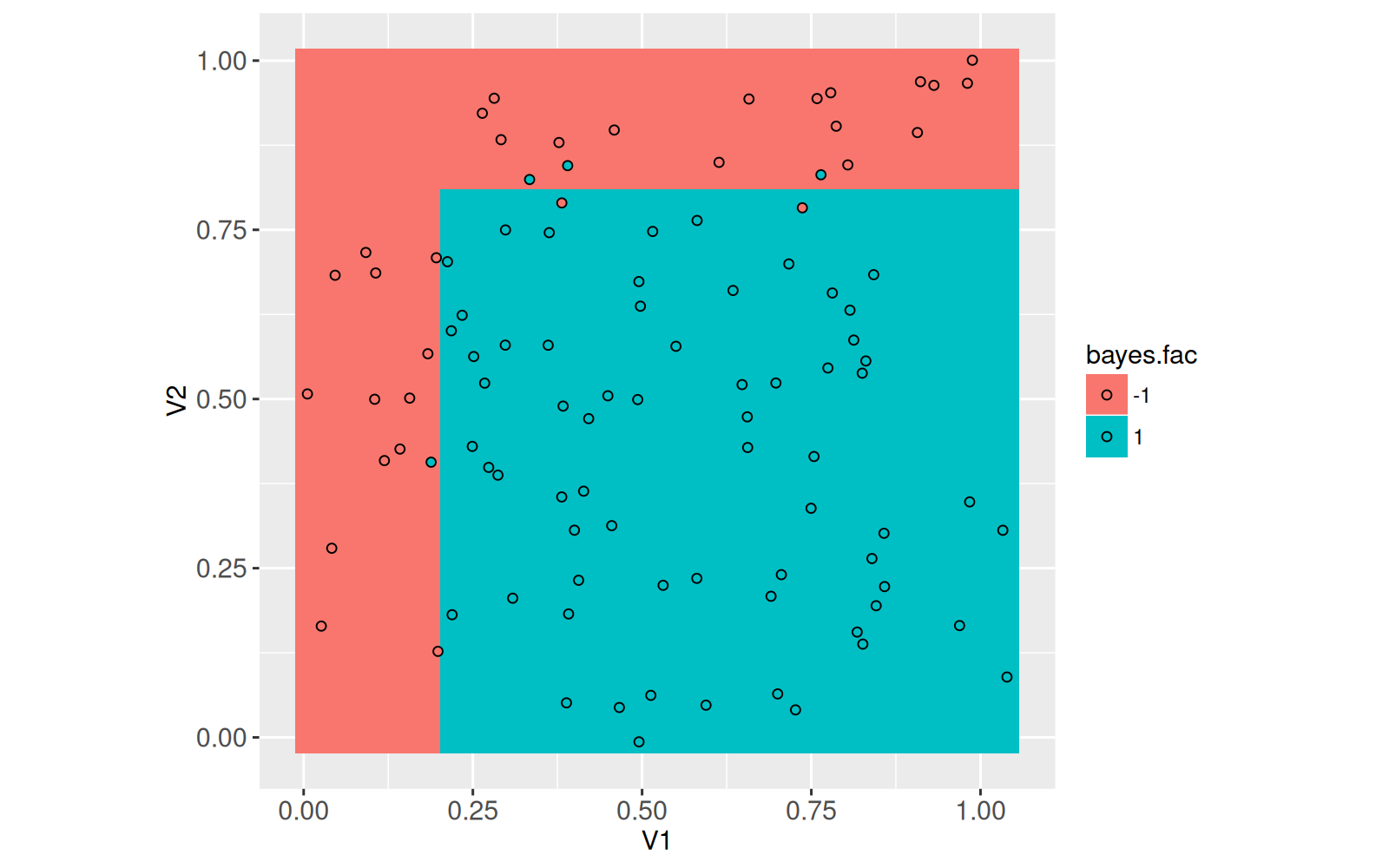
Le graphique ci-dessus montre que même en utilisant la meilleure fonction possible, il subsiste des erreurs de prédiction (points sur fond de couleur différente). Une autre façon de visualiser la meilleure fonction de classification est d’utiliser la limite de décision, qui peut être calculée à l’aide du code ci-dessous,
get_boundary <- function(score){
contour.list <- contourLines(
grid.list$V1, grid.list$V2,
matrix(
score,
length(grid.list$V1),
length(grid.list$V2),
byrow=TRUE),
levels=0)
if(length(contour.list)){
data.table(contour.i=seq_along(contour.list))[, {
with(contour.list[[contour.i]], data.table(level, x, y))
}, by=contour.i]
}
}
(bayes.contour.dt <- get_boundary(grid.dt$bayes.num)) contour.i level x y
1: 1 0 0.2016087 -0.006562821
2: 1 0 0.2016087 0.028166431
---
47: 1 0 1.0034601 0.809574611
48: 1 0 1.0390979 0.809574611La meilleure limite de décision est visualisée dans l’espace des caractéristiques ci-dessous,
ggplot()+
geom_path(aes(
x, y, group=contour.i),
data=bayes.contour.dt)+
geom_point(aes(
V1, V2, fill=label.fac),
color="black",
data=sim.dt)+
coord_equal()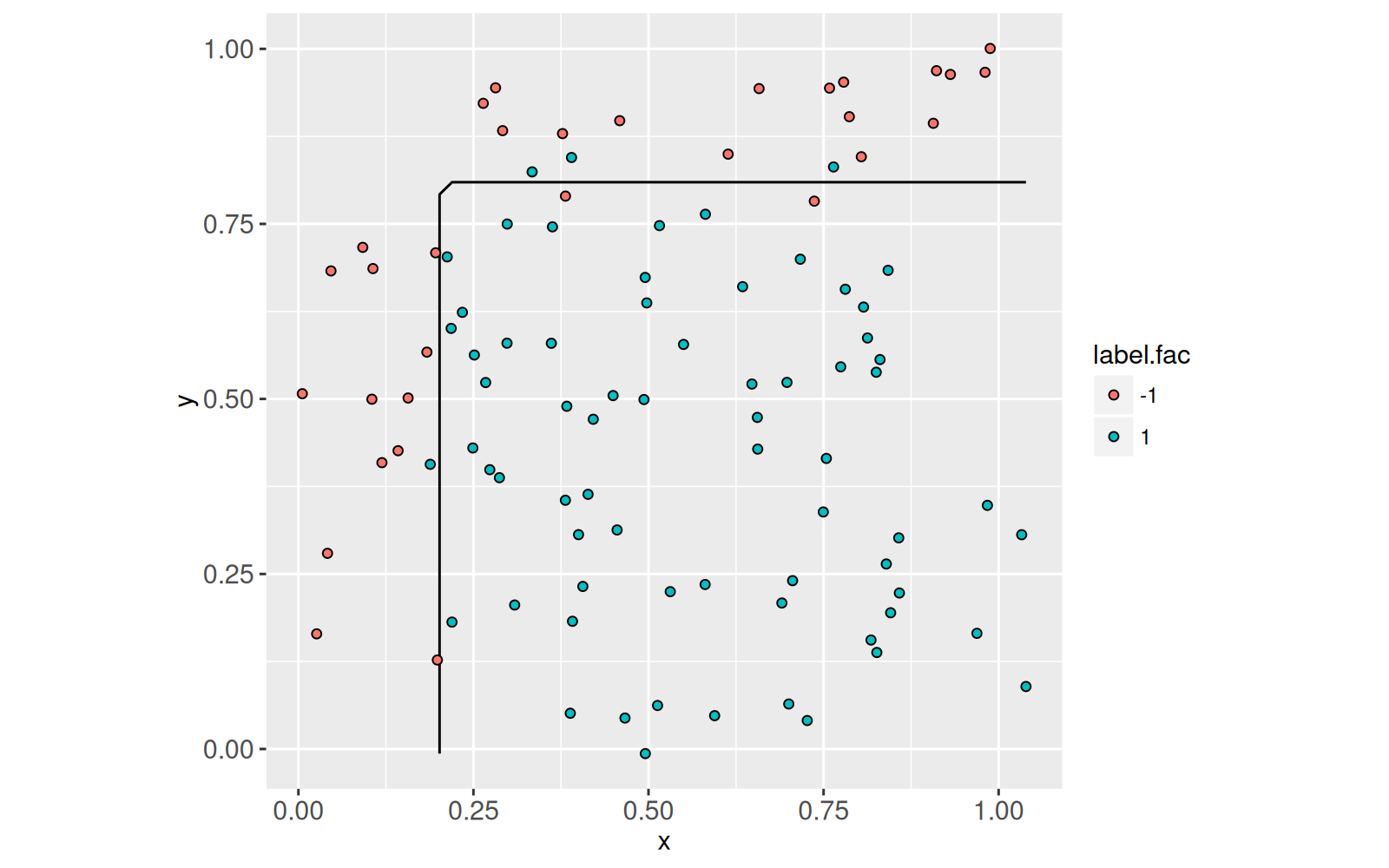
18.3 Propagation avant et arrière dans un modèle linéaire
Pour implémenter l’algorithme de descente de gradient pour l’apprentissage des paramètres du modèle de réseau de neurones, nous utiliserons un système simple d’auto-gradation. L’idée de l’auto-grad est que la structure du modèle de réseau neuronal doit être définie une seule fois et que cette structure doit être utilisée pour dériver les calculs de propagation vers l’avant (prédiction) et vers l’arrière (gradient). Nous utilisons ci-dessous un système auto-grad simple où chaque nœud du graphe de calcul est représenté par un environnement R (une structure de données mutable, nécessaire pour que les gradients soient rétropropagés à tous les paramètres du modèle). La fonction ci-dessous est un constructeur pour l’élément le plus élémentaire du système auto-grad, un nœud dans le graphe de calcul :
new_node <- function(value, gradient=NULL, ...){
node <- new.env()
node$value <- value
node$parent.list <- list(...)
node$backward <- function(){
grad.list <- gradient(node)
for(parent.name in names(grad.list)){
parent.node <- node$parent.list[[parent.name]]
parent.node$grad <- grad.list[[parent.name]]
parent.node$backward()
}
}
node
}Le code de la fonction ci-dessus commence par créer un nouvel environnement, puis le remplit avec trois objets :
-
valueest une matrice calculée par propagation vers l’avant à ce nœud du graphe de calcul. -
parent.listest une liste de nœuds parents, chacun d’entre eux étant utilisé pour calculervalue. -
backwardest une fonction qui doit être appelée par l’utilisateur sur le nœud final/de perte dans le graphe de calcul. Elle appellegradientqui doit calculer le gradient de la perte par rapport aux nœuds parents, qui sont stockés dans le fichiergraddans chaque nœud parent correspondant, avant d’appeler récursivementbackwardsur chaque nœud parent.
Le type de nœud le plus simple est le nœud initial, défini par le code ci-dessous,
initial_node <- function(mat){
new_node(mat, gradient=function(...)list())
}Le code ci-dessus indique qu’un nœud initial stocke simplement la matrice d’entrée mat comme valeur, et a une valeur gradient qui ne fait rien (parce que les nœuds initiaux dans le graphe de calcul n’ont pas de parents pour lesquels des gradients pourraient être calculés). Le code ci-dessous définit mm un noeud dans le graphe de calcul qui représente une multiplication de matrice,
Le mm ci-dessus suppose qu’il existe un nœud de pondération ayant le même nombre de lignes que le nombre de colonnes (plus une pour l’interception) dans le nœud de caractéristique. Les calculs d’avance/valeur et de gradient utilisent la multiplication matricielle. Par exemple, nous pouvons utilisermm pour définir un modèle linéaire simple,
num [1:50, 1] 0 0 0 0 0 0 0 0 0 0 ...On peut voir dans le code ci-dessus que l’élément mm renvoie un nœud représentant les valeurs prédites, un pour chaque ligne de la matrice des fonctions). Pour utiliser les caractéristiques de gradient, nous avons besoin d’une fonction de perte qui, dans le cas de la classification binaire, est la perte logistique (entropie croisée),
Le code ci-dessus définit la perte logistique et le gradient, en supposant que l’étiquette est soit -1, soit 1, et que la prédiction est un nombre réel (pas nécessairement entre 0 et 1, peut-être négatif). Le code ci-dessous crée des noeuds pour les étiquettes et la perte,
label.node <- initial_node(label.vec[is.set.list$subtrain])
loss.node <- log_loss(linear.pred.node, label.node)
loss.node$value[1] 0.6931472Maintenant que nous avons calculé la perte, nous pouvons calculer le gradient de la perte par rapport aux pondérations, qui est utilisé pour effectuer les mises à jour pendant l’apprentissage. Rappelez-vous que nous devons maintenant appelerbackward (sur la perte de soustraction), qui devrait finalement stocker le gradient en tant que weight.node$grad. Ci-dessous, nous vérifions d’abord qu’il n’a pas encore été calculé, puis nous le calculons :
weight.node$gradNULLloss.node$backward()
weight.node$grad [,1]
[1,] -0.16000000
[2,] -0.10511619
[3,] -0.02447615Notez que, puisque loss.node contient des références récursives à ses nœuds parents (y compris les prédictions et les pondérations), l’élément backward ci-dessus est capable de calculer et de stocker de manière pratique les données de l’appel weight.node$grad le gradient de la perte par rapport aux paramètres de pondération. Le gradient est la direction de la montée la plus raide, ce qui signifie que les pondérations de direction pourraient être modifiées pour maximiser la perte. Comme nous voulons minimiser la perte, l’algorithme d’apprentissage effectue des mises à jour dans la direction du gradient négatif, de la descente la plus raide.
(descent.direction <- -weight.node$grad) [,1]
[1,] 0.16000000
[2,] 0.10511619
[3,] 0.02447615En descente de gradient pour ce modèle linéaire, nous mettons à jour le vecteur de pondération dans cette direction. Chaque mise à jour du vecteur de pondération est appelée itération ou étape. Un petit pas dans cette direction garantit une diminution de la perte, mais un pas trop petit ne permet pas de faire beaucoup de progrès vers la minimisation de la perte. On ne sait pas jusqu’où il est préférable d’aller dans cette direction, c’est pourquoi il faut généralement chercher dans une grille de tailles de pas (ou de taux d’apprentissage). Nous pouvons également effectuer une recherche linéaire, c’est-à-dire tracer le graphique suivant de la perte en fonction de la taille du pas, puis choisir la taille du pas avec la perte minimale.
(line.search.dt <- data.table(step.size=seq(0, 10, l=101))[, .(
loss=log_loss(mm(
feature.node,
initial_node(weight.node$value+step.size*descent.direction)
), label.node)$value
), by=step.size]) step.size loss
1: 0.0 0.6931472
2: 0.1 0.6894865
---
100: 9.9 0.8490474
101: 10.0 0.8543739line.search.min <- line.search.dt[which.min(loss)]
ggplot()+
geom_line(aes(
step.size, loss),
data=line.search.dt)+
geom_point(aes(
step.size, loss),
data=line.search.min)+
geom_text(aes(
step.size, loss, label=sprintf(
"min loss=%f at step size=%.1f",
loss, step.size)),
data=line.search.min,
size=4,
hjust=0,
vjust=1.5)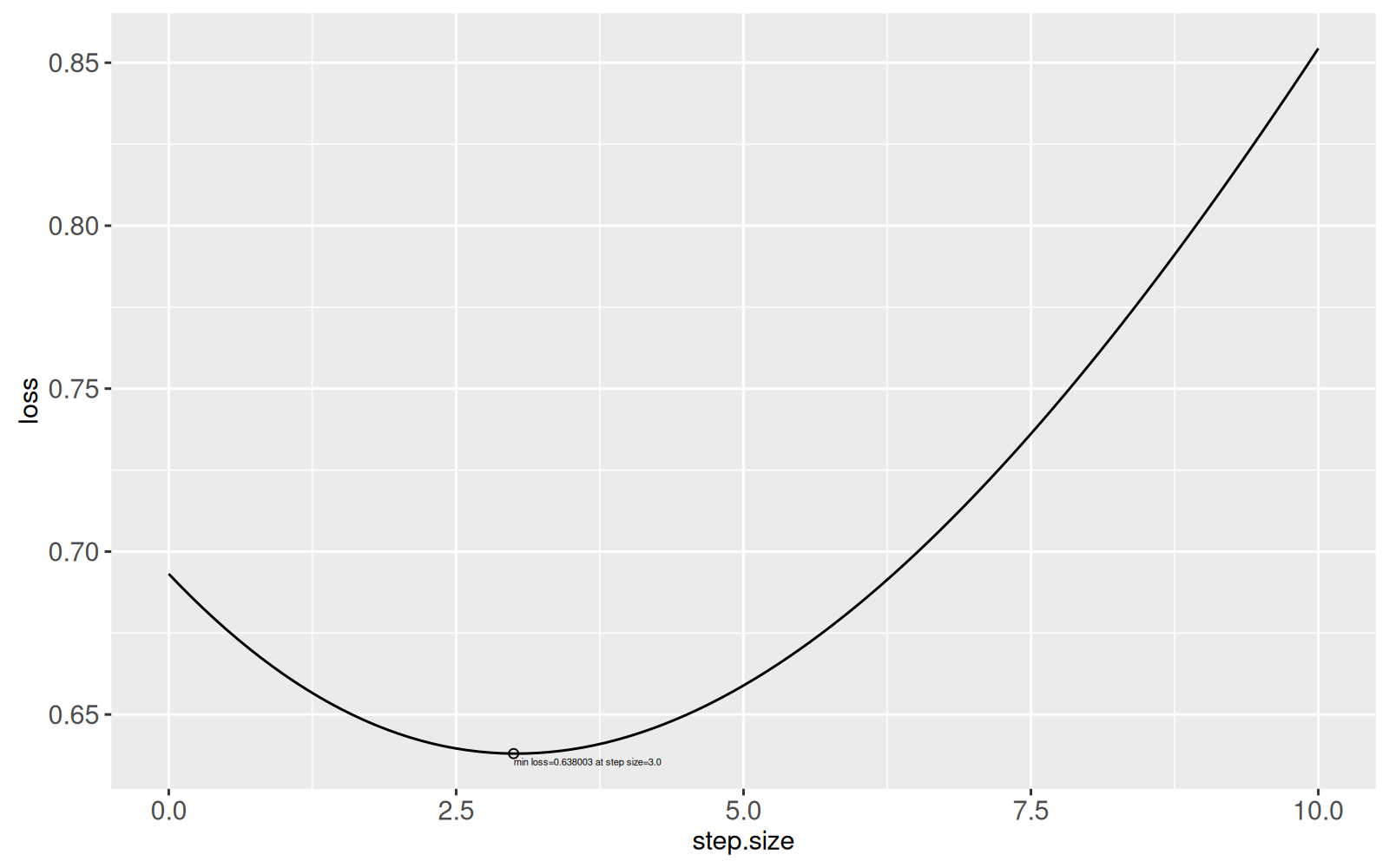
Le graphique ci-dessus montre que la perte minimale se produit à une taille de pas d’environ 3, ce qui signifie que la recherche linéaire choisirait cette taille de pas pour cette mise à jour/itération des paramètres de descente de gradient, avant de recalculer le gradient à l’itération suivante.
18.4 Apprentissage par réseau neuronal
La définition d’un modèle linéaire dans la section précédente était relativement simple, car il n’y a qu’un seul paramètre de matrice de pondération (en fait, un vecteur de pondération, avec le même nombre d’éléments que le nombre de colonnes/caractéristiques, plus un pour l’ordonnée à l’origine). En revanche, un réseau neuronal a plus d’un paramètre de matrice de pondération à apprendre. Nous initialisons ces pondérations sous forme de nœuds dans le code ci-dessous,
new_weight_node_list <- function(units.per.layer, intercept=TRUE){
weight.node.list <- list()
for(layer.i in seq(1, length(units.per.layer)-1)){
input.units <- units.per.layer[[layer.i]]+intercept
output.units <- units.per.layer[[layer.i+1]]
weight.mat <- matrix(
rnorm(input.units*output.units), input.units, output.units)
weight.node.list[[layer.i]] <- initial_node(weight.mat)
}
weight.node.list
}
(units.per.layer <- c(ncol(features.noisy), 40, 1))[1] 2 40 1(weight.node.list <- new_weight_node_list(units.per.layer))[[1]]
<environment: 0x563171cba768>
[[2]]
<environment: 0x563171cbd450>[[1]]
[1] 3 40
[[2]]
[1] 41 1La sortie ci-dessus montre qu’il y a une seule couche avec 40 unités cachées dans le réseau neuronal, ce qui signifie qu’il y a deux matrices de pondération à apprendre. Chacune de ces matrices de pondération est utilisée pour prédire les unités d’une couche donnée, à partir des unités de la couche précédente. Afin d’apprendre une fonction de prédiction qui est une fonction non linéaire des caractéristiques, chaque couche, à l’exception de la dernière, doit avoir une fonction d’activation non linéaire, appliquée élément par élément aux unités après la multiplication de la matrice.
Par exemple, une fonction d’activation non linéaire courante et efficace est la ReLU (Rectified Linear Units), qui est implémentée ci-dessous,
num [1:50, 1:40] 1.62 3.67 2.34 2.42 1.57 ...hidden.before.act$value[1:5,1:5] [,1] [,2] [,3] [,4] [,5]
[1,] 1.617099 -0.31485515 0.8687167 0.5969050 -0.5717334
[2,] 3.665478 -0.08953216 1.1884750 0.7686507 -0.7655569
[3,] 2.335856 -1.53696561 1.1271410 0.4960481 -1.2771119
[4,] 2.418533 -0.61750628 1.0377415 0.6157081 -0.8390015
[5,] 1.571396 1.26836784 0.6830969 0.7897418 0.2105804hidden.after.act <- relu(hidden.before.act)
hidden.after.act$value[1:5,1:5] [,1] [,2] [,3] [,4] [,5]
[1,] 1.617099 0.000000 0.8687167 0.5969050 0.0000000
[2,] 3.665478 0.000000 1.1884750 0.7686507 0.0000000
[3,] 2.335856 0.000000 1.1271410 0.4960481 0.0000000
[4,] 2.418533 0.000000 1.0377415 0.6157081 0.0000000
[5,] 1.571396 1.268368 0.6830969 0.7897418 0.2105804Notez dans la sortie ci-dessus que l’activation ReLU met les valeurs négatives à zéro et maintient les valeurs positives inchangées :
(relu.dt <- data.table(
input=seq(-5, 5, l=101)
)[, output := relu(initial_node(input))$value][]) input output
1: -5.0 0.0
2: -4.9 0.0
---
100: 4.9 4.9
101: 5.0 5.0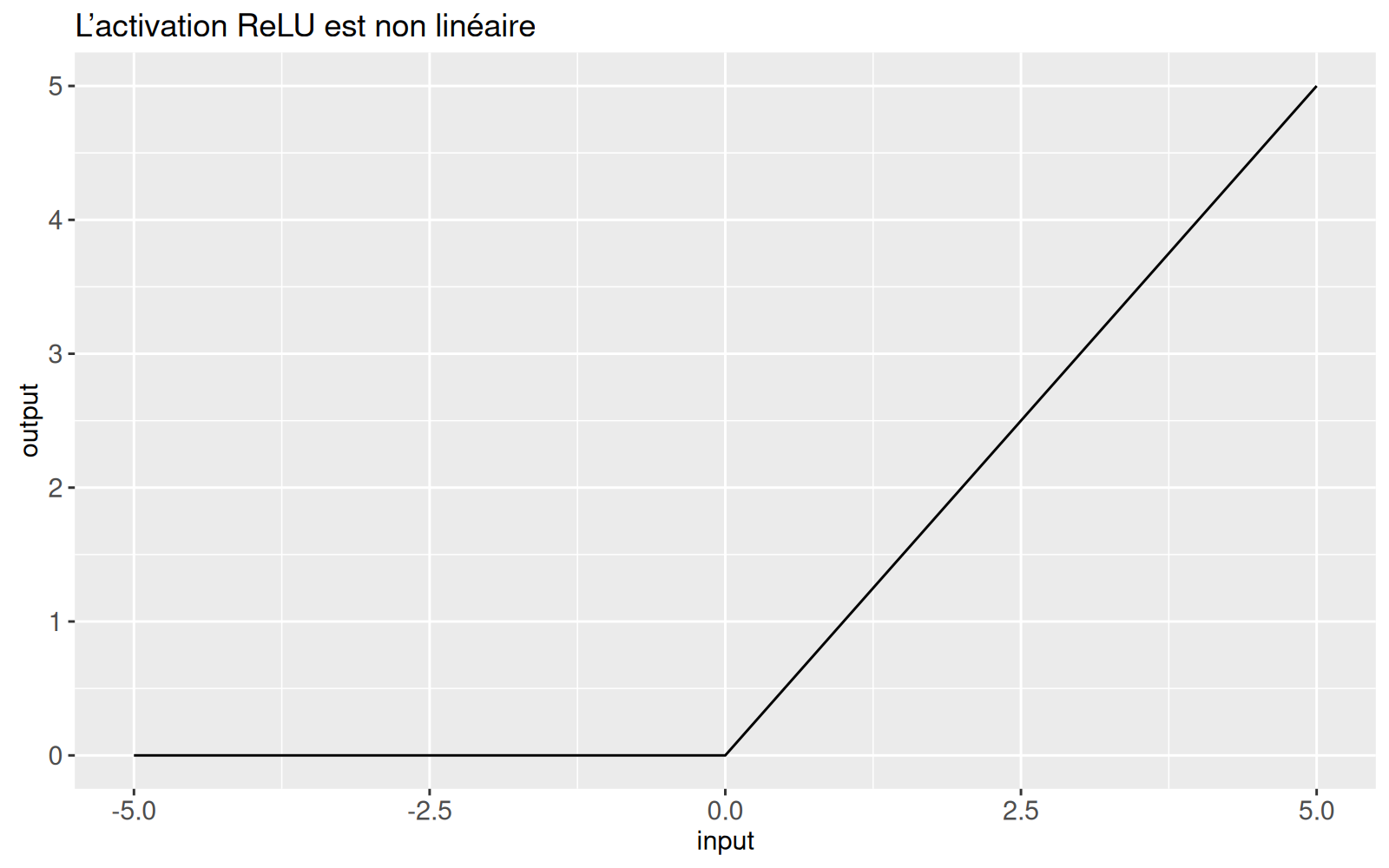
Enfin, le dernier nœud dont nous avons besoin pour implémenter notre réseau neuronal est un nœud pour les prédictions, calculé via la boucle for sur les nœuds de pondération dans la fonction ci-dessous,
pred_node <- function(set.features){
feature.node <- initial_node(set.features)
for(layer.i in seq_along(weight.node.list)){
weight.node <- weight.node.list[[layer.i]]
before.node <- mm(feature.node, weight.node)
feature.node <- if(layer.i < length(weight.node.list)){
relu(before.node)
}else{
before.node
}
}
feature.node
}
nn.pred.node <- pred_node(features.noisy[is.set.list$subtrain,])
str(nn.pred.node$value) num [1:50, 1] 3.85 6.42 2.14 3.54 8.18 ...Le pred_node est également utile pour calculer les prédictions sur la grille de caractéristiques, ce qui sera utile plus tard pour visualiser la fonction apprise,
num [1:900, 1] 1.74 2.09 2.43 2.78 3.12 ...Le code ci-dessous combine tous les éléments ci-dessus dans un algorithme d’apprentissage par descente de gradient. Les hyperparamètres sont la taille du pas constant et le nombre maximum d’itérations.
step.size <- 0.5
max.iterations <- 1000
units.per.layer <- c(ncol(features.noisy), 40, 1)
loss.dt.list <- list()
err.dt.list <- list()
pred.dt.list <- list()
set.seed(10)
weight.node.list <- new_weight_node_list(units.per.layer)
for(iteration in 1:max.iterations){
loss.node.list <- list()
for(set in names(is.set.list)){
is.set <- is.set.list[[set]]
set.label.node <- initial_node(label.vec[is.set])
set.features <- features.noisy[is.set,]
set.pred.node <- pred_node(set.features)
set.loss.node <- log_loss(set.pred.node, set.label.node)
loss.node.list[[set]] <- set.loss.node
set.pred.num <- ifelse(set.pred.node$value<0, -1, 1)
is.error <- set.pred.num != set.label.node$value
err.dt.list[[paste(iteration, set)]] <- data.table(
iteration, set,
set.features,
label=set.label.node$value,
pred.num=as.numeric(set.pred.num))
loss.dt.list[[paste(iteration, set)]] <- data.table(
iteration, set,
mean.log.loss=set.loss.node$value,
error.percent=100*mean(is.error))
}
grid.node <- pred_node(grid.mat)
pred.dt.list[[paste(iteration)]] <- data.table(
iteration,
grid.dt,
pred=as.numeric(grid.node$value))
loss.node.list$subtrain$backward()#<-back-prop.
for(layer.i in seq_along(weight.node.list)){
weight.node <- weight.node.list[[layer.i]]
weight.node$value <- #learning/param updates:
weight.node$value-step.size*weight.node$grad
}
}
loss.dt <- rbindlist(loss.dt.list)
err.dt <- rbindlist(err.dt.list)
pred.dt <- rbindlist(pred.dt.list)
loss.tall <- melt(loss.dt, measure=c("mean.log.loss", "error.percent"))
loss.tall[, log10.iteration := log10(iteration)]
min.dt <- loss.tall[
, .SD[which.min(value)], by=.(set, variable)]
ggplot()+
facet_grid(variable ~ ., scales="free")+
scale_y_continuous("")+
geom_line(aes(
iteration, value, color=set),
data=loss.tall)+
geom_point(aes(
iteration, value, fill=set),
color="black",
data=min.dt)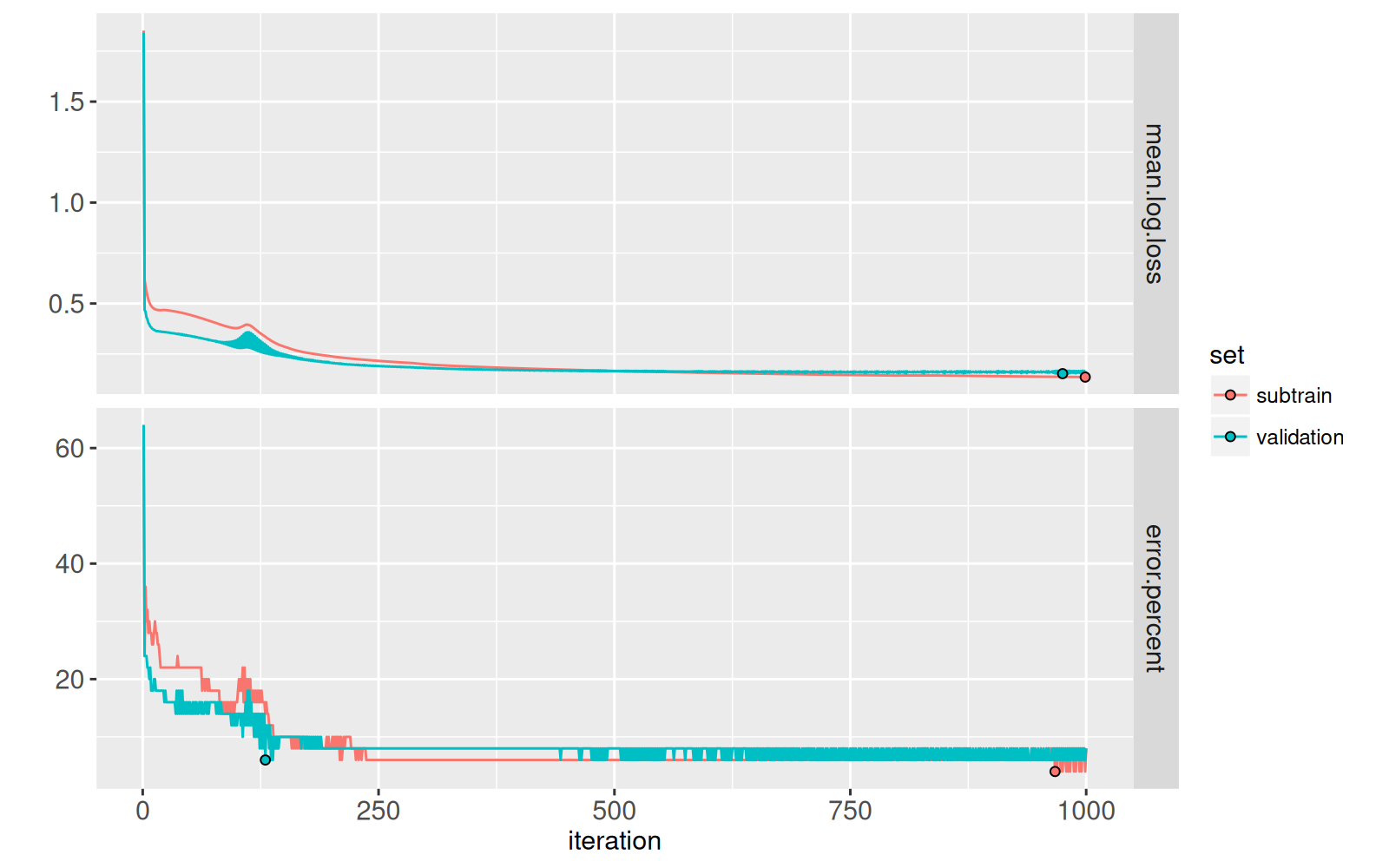
Dans le code ci-dessus, nous avons enregistré les pertes et les prédictions pour toutes les itérations de la descente de gradient, mais dans le code ci-dessous, nous ne visualisons que certaines d’entre elles, en raison de l’espace limité :
some <- function(DT)DT[iteration%in%c(1,5,10,50,100)]
err.dt[, prediction := ifelse(label==pred.num, "correct", "error")]
iteration.contours <- pred.dt[
, get_boundary(pred), by=.(iteration)]
some.loss <- some(loss.dt)
pred.dt[, norm.pred := pred/max(abs(pred)), by=.(iteration)]
some.pred <- some(pred.dt)
some.err <- some(err.dt)
some.contours <- some.pred[
, get_boundary(pred), by=.(iteration)]
ggplot()+
facet_grid(set ~ iteration, labeller="label_both")+
geom_tile(aes(
V1, V2, fill=norm.pred),
color=NA,
data=some.pred)+
geom_path(aes(
x, y, group=contour.i),
color="grey50",
data=some.contours)+
scale_fill_gradient2()+
geom_point(aes(
V1, V2, color=prediction, fill=label/2),
size=2,
data=some.err)+
scale_color_manual(
values=c(correct="white", error="black"))+
coord_equal()+
scale_y_continuous(breaks=seq(0,1,by=0.5))+
scale_x_continuous(breaks=seq(0,1,by=0.5))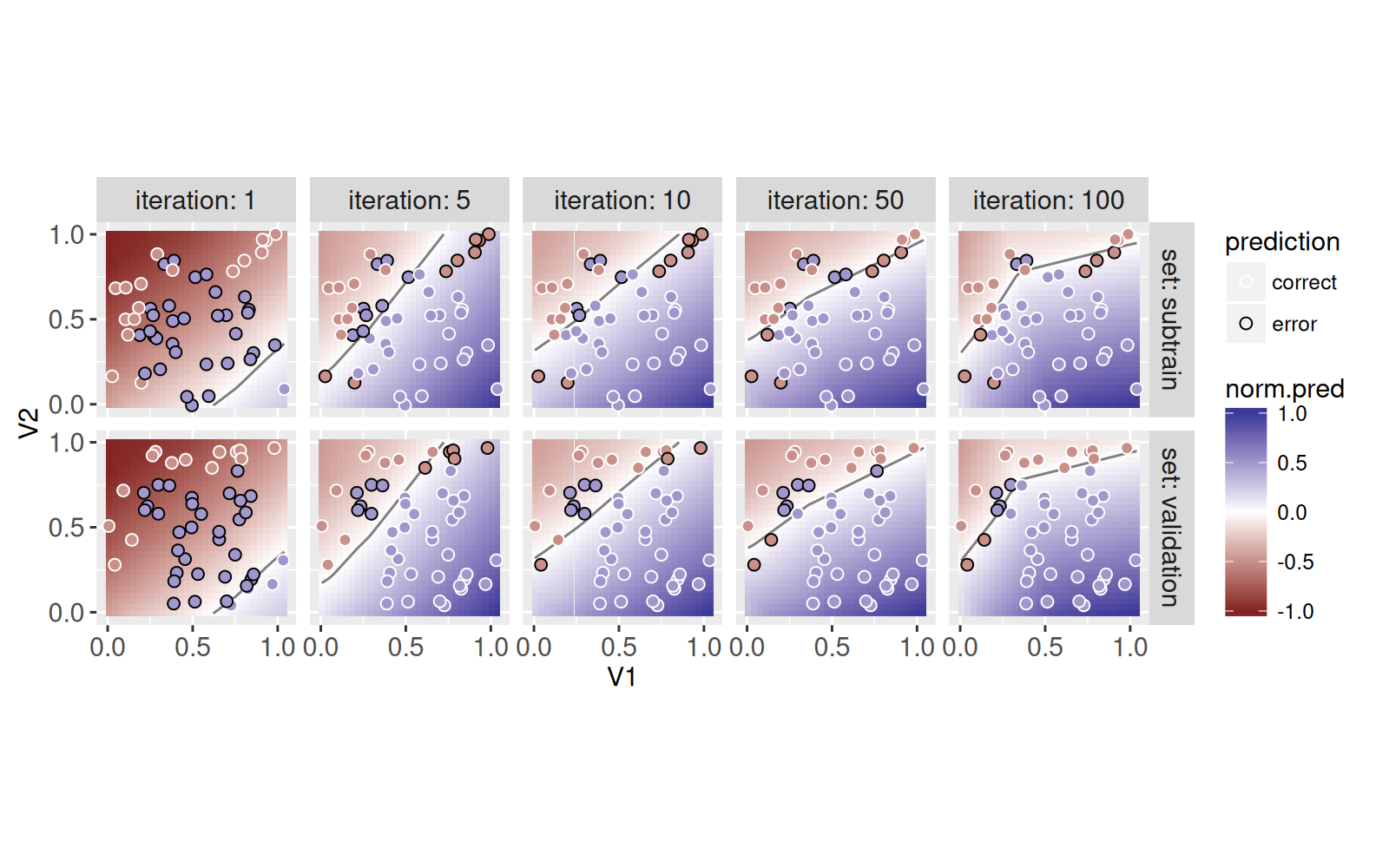
Le graphique ci-dessus montre qu’au fur et à mesure que le nombre d’itérations augmente, les prédictions deviennent plus précises. Enfin, nous terminons par un graphique interactif dans lequel vous pouvez cliquer sur le graphique des pertes pour sélectionner une itération de descente de gradient, pour laquelle la limite de décision correspondante est affichée sur le graphique des prédictions.
n.subtrain <- sum(is.set.list$subtrain)
loss.dt[, n.set := ifelse(
set=="subtrain", n.subtrain, sim.row-n.subtrain
)][, error.count := n.set*error.percent/100]
it.by <- 10
some <- function(DT)DT[iteration %in% as.integer(
seq(1, max.iterations, by=it.by))]
animint(
title="Réseau de neurones vs modèle linéaire",
out.dir="neural-networks-sim",
loss=ggplot()+
ggtitle("Courbes de perte/erreur, cliquer pour sélectionner le modèle/l’itération")+
theme_bw()+
theme_animint(width=600, height=350)+
theme(panel.margin=grid::unit(1, "lines"))+
facet_grid(variable ~ ., scales="free")+
scale_y_continuous("")+
scale_x_continuous(
"Itération/époque d’entraînement")+
geom_line(aes(
iteration, value, color=set, group=set),
data=loss.tall)+
geom_point(aes(
iteration, value, fill=set),
color="black",
data=min.dt)+
geom_tallrect(aes(
xmin=iteration-it.by/2,
xmax=iteration+it.by/2),
alpha=0.5,
clickSelects="iteration",
data=some(loss.tall[set=="subtrain"])),
data=ggplot()+
ggtitle("Fonction apprise au modèle/à l’itération sélectionné(e)")+
theme_bw()+
theme_animint(width=600)+
facet_grid(. ~ set, labeller="label_both")+
geom_tile(aes(
V1, V2, fill=norm.pred),
color=NA,
showSelected="iteration",
data=some(pred.dt))+
geom_text(aes(
0.5, 1.1, label=paste0(
"loss=", round(mean.log.loss, 4),
", ", error.count, "/", n.set,
" errors=", error.percent, "%")),
showSelected="iteration",
data=loss.dt)+
geom_path(aes(
x, y, group=contour.i),
showSelected="iteration",
color="grey50",
data=some(iteration.contours))+
geom_point(aes(
V1, V2, fill=label/2, color=prediction),
showSelected=c("iteration", "set"),
size=4,
data=some(err.dt))+
scale_fill_gradient2(
"Class/Score")+
scale_color_manual(
values=c(correct="white", error="black"))+
scale_x_continuous(
"Input/Feature 1")+
scale_y_continuous(
"Input/Feature 2")+
coord_equal())18.5 Résumé du chapitre et exercices
Exercices :
- Ajouter l’animation sur le nombre d’itérations.
- Ajouter des transitions graduelles lors du changement du nombre d’itérations sélectionné.
- Ajoutez une boucle for sur des graines aléatoires (ou des plis de validation croisée) dans l’étape de division des données, et créez une visualisation qui montre comment cela affecte les résultats.
- Ajoutez une boucle for sur des graines aléatoires à l’étape d’initialisation de la matrice de pondération, et créez une visualisation qui montre comment cela affecte les résultats.
- Calculez les résultats pour une autre architecture de réseau neuronal (et/ou un modèle linéaire, en ajoutant une boucle for sur différentes valeurs de
units.per.layer). Ajouter un autre graphique ou une facette permettant de sélectionner l’architecture du réseau neuronal et de comparer facilement la perte de validation minimale entre les modèles (par exemple, ajouter des colonnes de facettes au graphique de perte et ajouter des lignes horizontales pour mettre en évidence la perte minimale). - Modifiez l’algorithme d’apprentissage pour utiliser la recherche linéaire plutôt qu’une taille de pas constante, puis créez une visualisation qui compare les deux approches en termes de perte de validation minimale.
Suivant, Chapitre 19 explique comment visualiser les valeurs de P, y compris comment contourner le surdimensionnement, à l’aide d’une carte thermique liée à un graphique de dispersion zoomé. .